Table of Contents
Dynamic simulation of a building's thermal performance
Dynamic Simulation using DYNBIL
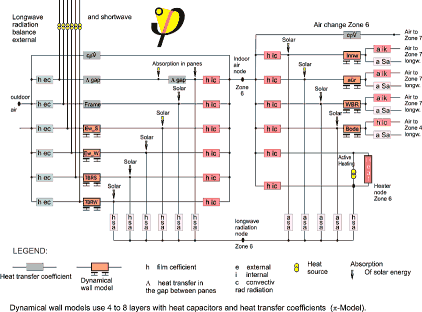 |
| Fig. 1 A typical room model used in instationary simulation of a buildings thermal performance; this is the model-type used in the program DYNBIL [Feist 1994] |
Dynbil is a multizone dynamic thermal building simulation program developed at the Passive House Institute. Dynbil also takes into account moisture storage and moisture transport processes. The room model works with one air node and one radiation node, which are clearly separated from each other. Heat transmitted to interior surfaces is calculated depending on the location in the room and the actual temperature difference; for exterior surfaces, the complete solar and infrared radiation balance and the influence of wind speed are taken into account. Heat transfer (radiative and convective/conductive) and g-values are calculated for windows depending on the current temperature and solar radiation in each period of time (nonlinear). The wall model uses not transfer functions but uses a forward difference method, thereby fulfilling the conservation of energy principle even over long periods of time. The program was first validated under Central and North European climatic conditions with a number of construction projects measured in detail.
A single room (“zone”) will be modelled by DYNBIL as shown in fig. 1.
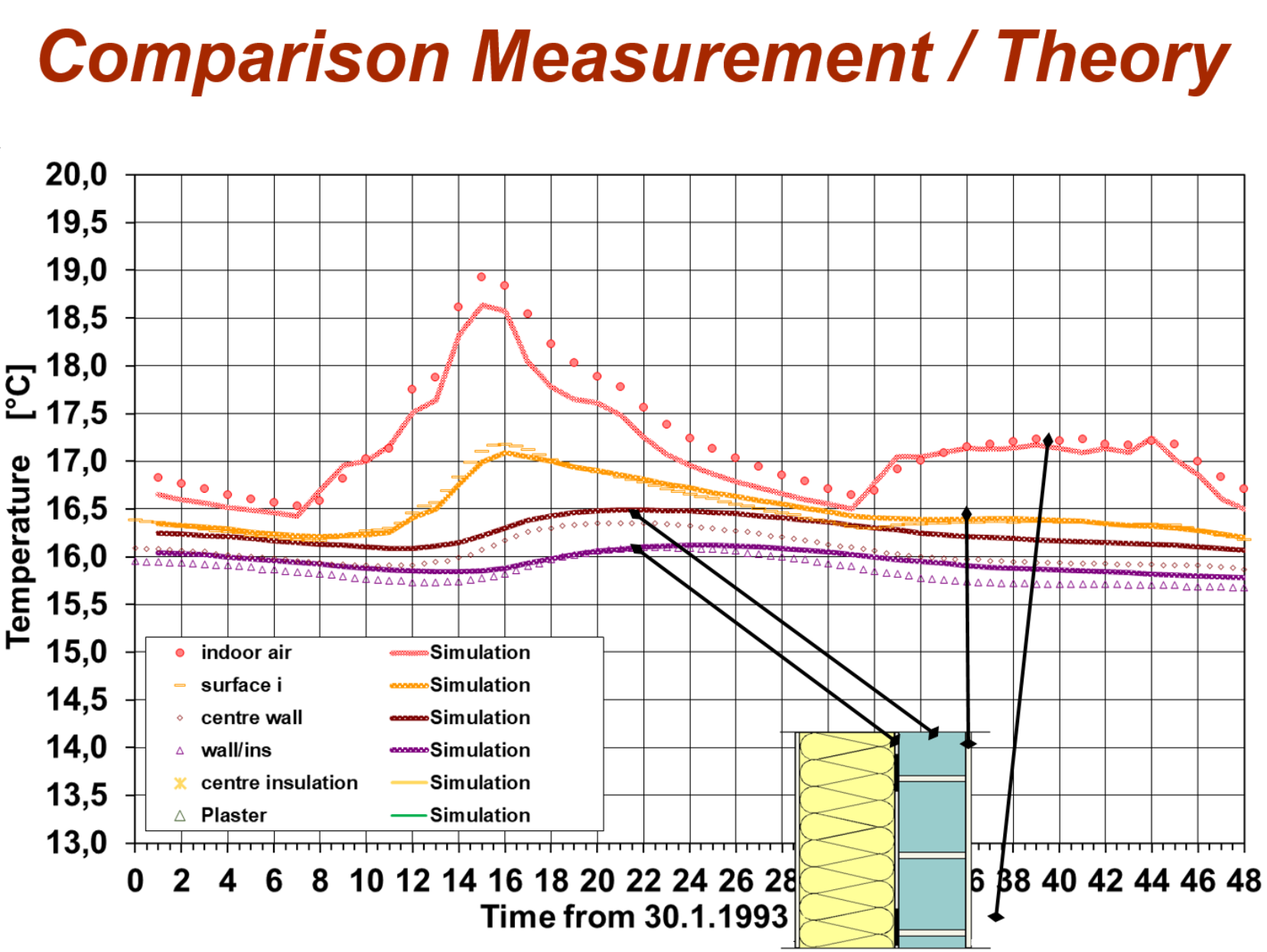
In the meantime, additional features have been added such as simulations of moisture transport and ventilation models. Although DYNBIL models the building components very accurately (see e.g. comparison of simulated and measured temperatures within the wall), the focus is the whole building perspective (fig. 2). The entire building defines the system boundary. All energy fluxes are part of the model, including all electric appliances. This makes it possible to simulate the internal heat gains. General assumptions on heat gains may be tolerable for energy inefficient buildings, but lead to high differences in the calculated demand as soon as heating and/or cooling demands are very low. Another aspect of the whole building approach is the integration of all system components including the consideration of thermal comfort, ventilation, air quality, noise protection, user friendliness, building protection.
 |
| Fig. 2 Several zones will be connected to a building model with air flows between the zones as well as components connecting the different zones. |
Dynbil has been validated with the detailed measurements in the first Passive House (located in Darmstadt Kranichstein; see fif. 3). It had been possible to predict the energy consumptions, as well as to test several variations of the model itself. DYNBIL is also the basis for the development of stationary tools.
General Considerations on Models used for Simulation
The actual task in dealing with the questions of indoor climate and energy balance results from the high level of complexity which the “house and heating” system exhibits in combination with the respective physical theories of the subsystems.
The mathematical models for mapping the subsystems are largely “simple” and proven: the heat conduction in solids and non-flowing fluids can be described by Fourier's dynamic heat conduction equation, convection in space is dealt with by the equations of Navier-Stokes, radiation is determined according to Planck's law of radiation - etc. The respective basic equations mentioned here generally result in coupled, non-linear, partial differential equations of 2nd order in space and time, taking into account the temperature dependence of the coefficients. However, boundary conditions encountered in buildings require considerable effort even for a single subsystem (e.g. the gas space of a double-pane insulation glazing). This has its cause
- on the one hand in the complexity of the basic equilibria involved (e.g. with Navier Stokes),
- on the other hand especially in the present boundary conditions, e.g. the generally not simple geometries of components.
While a solution to the flow problem for a room in a stationary case can be tackled numerically with some effort today using the Navier-Stokes equations, a solution to the overall problem “building & heating” in the coupling of all appropriate physical theories (“first principles”) today still exceeds every reasonable computation capacity.
On the contrary, the task is to reduce the complexity again by decisive simplifications in the parts constituting the overall model to such an extent that treatment with reasonable effort is always the path to take.
It is clear from the task that the model must map all the essential, interacting components of the building and the heating system: each sub-model must be dealt with under the boundary conditions that are significantly determined by the other components. This is one of the theses that will be substantiated at various points in this publication - two examples:
- The energy balance of a window surface depends not only on the component “window” itself, but also on the other components of the room (in particular their insulation and their storage capacity on the room side) and on the operation of ventilation and heating systems,
- The assessment of components for solar energy use (such as transparent heat insulation) with regard to the energy balance to be achieved all year round depends on the (insulation) standard of the building in which the subsystem is used.
An image of the overall “Building & Heating” system is therefore indispensable for the investigations provided here. However, in order to reduce the complexity of the model, it is conceivable to reduce the level of detail of the model formation for the individual components: it only has to be guaranteed that the interactions between the components are adequately represented stay. As a result, for any desired, more precise detailed examinations, it remains at liberty to extract the boundary conditions for individual components from the (coarser) overall model and to use them for detailed individual models of components.
Special features of the computer-aided simulation
The mathematical model for the treatment of the thermal behavior of buildings is characterized by a high level of complexity as shown in the last section: a whole series of partial models for
- Instationary heat conduction (Fourier equation),
- The flow of air in space (Navier-Stokes equations),
- The radiation exchange between components (Planck law),
- The reflection, transmission and absorption of solar radiation,
- Control of heating,
- Free heat sources in the room,
- Infiltration and ventilation
are to be treated and linked. This is done geometrically with generally omplex boundary conditions (geometry of a building) and the climate as an inhomogeneity.
Even with simple sub-models (such as the connections of different components, e.g. on the eaves), the mathematical sub-model (e.g. Fourier problem with boundary conditions) can no longer be solved analytically. Already here you have to rely on numerical methods for the solution. To implement such numerical methods, computer algorithms are expediently used today.
Such a computer algorithm can also be understood as a (program-based) model of the mathematical model: in this respect the use of computer simulation does not mean a principient innovation compared to the mathematical models generally introduced in the natural sciences. It goes without saying that discretization errors and numerical errors must be carefully discussed here - they characterize the deviation between the mathematical model and the model formation with the underlying program. In this case, however, the model relationship is comparatively simple: it can be formulated internally between the algorithm of the program and the mathematical model and is therefore even accessible to mathematical methods of proof.
Quite often, therefore, even with computer supported simulation models, the “detour” via an abstractly defined mathematical model is no longer described, rather the model is formulated directly as a program. In the first place, too, this is not a fundamental deviation from the path of virtue in scientific theories - after all, not every model has to be a mathematical one and, in addition, computer algorithms are also mathematical models. However, there are some dangers in this shortened procedure:
- As a rule, the digital algorithm itself lacks direct clarity (it is mastered by discretion). Therefore, even experienced users often find it difficult to read simple facts that can be generalized from EDP models.
Example:
In the numerical solution of simple differential equations (dy/dt = - ω²y) the realization that simple solutions y(t) = a cos (ωt) + b sin (ωt) exist will usually be blurred. This solves the problem numerically, but it spills a better understanding.
- By circumventing the mathematical model formulation under certain circumstances, physically important system properties are also hidden.
Example:
Conservation theorems that follow from symmetry groups and that are easy to derive in mathematical field formulation also work in the numerical model
- Even from the greatest abundance of numerical “case studies”, no strong evidence of hypotheses can be drawn: even in the case of general legality, the relationship at this level of model examination therefore similarly remains on a basis of table-based validation instructed like the model-system relationship in metrologically recorded systems. We are faced with this dilemma in large parts of the studies on the building model: even the parameter studies, which are carried out in [Feist 1994] with great effort, are not suitable for proving the validity of the model - they can only, hint to a progressive validation of physical models and increase confidence in the usability of the simulation models.
The advantage of using adequate mathematical models (and the resulting possibility of verifying an computer aided algorithm over the mathematical model) is therefore obvious. But there are also practical advantages in favor of such a route: numerical mathematics often offers different methods for the algorithmic treatment of the same mathematical problem, which are useful depending on the circumstances. In this way, computing time and storage space can be saved.
As a result of the complexity of the problem, the consequent priority for a clean mathematical formulation is not always observed in this work before it is used in IT algorithms. Closing the remaining gaps remains a task for further investigations.
Simulation as an alternative to measuring?
According to the explanations in the last sections, such a question does not arise: simulation and measurement have different functions in the cognitive process and complement each other. The simulation can neither make measurements completely superfluous (validation of models is only possible via measurements) - nor is it practical and sensible to want to answer all questions by measurements (statements that can be generalized can never be obtained by at most a finite number of measurements).
Especially in the field of research into the thermal behavior of buildings, there is a widespread basic skepticism about simulation: Many practitioners only trust statements about the annual heating requirements of houses if they are validated by “measurements”. Here, however, a critical evaluation of measurements would be appropriate:
- According to the results already available today, the heating requirement is extremely sensitive to a number of parameters that can be changed by the user (eg the internal temperature and the air exchange). Measurements are therefore only to be regarded as usful data source if these parameters are also recorded in a suitable manner (e.g. internal temperature profile, tracer gas measurement of the air exchange) or checked in some other way (e.g. by permanently setting them with control organs) or by measurements within very large samples. (All these paths have been used in the development of passive houses.)
- The dependency on the external climate is also very high: In different years at the same Central European location (e.g. in Frankfurt am Main) the annual consumption of the same building can deviate by more than 50% with the same user behavior. Measured values can therefore only be compared if they relate to the same climate. Realizing this is quite difficult: without resorting to arithmetic corrections (the theoretical models need a basis: the usually used heating degree day correction is a very primitive and a quite questionable model), this can only be done by simultaneous measurements at the same place.
- In addition, inaccuracies in the measurement itself must be expected: “If you measure, you measure manure”. The reliable measurement of building physics parameters is an art in itself. E.g. even monitoring indoor air temperatures requires good knowledge of the theory (shielding the sensor against radiation, time constant of the sensor, self-heating, long-term stability …). Consumption value measurements are often based on volume or volume flow probes (gas, oil, hot water). Volume flow meters often have offset volume flows below which they do not run or are extremely inaccurate. Such aspects must be carefully observed during measurements - this is possible, but often increases the effort significantly beyond what is common today. It is therefore only justified to rely on measured values if one knows exactly how the measurement was made.
Typical examples of questions that arise in energy related building planning are the following:
- Is it worthwhile to increase the proportion of south windows in a building from 50 to 60% in order to save heating energy?
- How is the indoor climate influenced in summer by changing the color of the outer facade?
Questions of these types can also be asked regarding the window structure, the floor covering, the roof construction and the like. From the parameter studies documented in [Feist 1994], it follows that the influence of each of these individual parameters on the annual heating consumption is not very high (e.g. we expect (1) to relate to a building with Swedish building standard 1980 result in a saving of 5.6% with triple glazing). The change in consumption, which occurs in the same building when the central interior temperature changes by only half a degree Celsius, is approximately the same: should the question posed experimentally with the help If measurements be answered with an accuracy of about 5%, the inside (and of course also the outside climate) of the two test houses would have to agree within about 0.025 K (!) (average temperatures). Such a requirement is in principle conceivable with high control precision and extremely good measurement technology for unoccupied buildings which are otherwise adjacent to one another in an otherwise identical construction - but with an unacceptable amount of effort. As a before-and-after measurement on the same building (in subsequent years with different climatic conditions), such a comparison is impossible: the back calculation to a “standard climate” would have to be done using the theoretical models that we wanted to avoid by such a measurement project.
The situation is also comparable with (2): the differences that occur due to different window positions, especially at night in the summer indoor climate, are many times greater than the influence that is actually to be examined.
The examples dealt with show that questions such as (1) or (2) that are decisive for building planning can only be answered by direct field measurements in question with unacceptable effort or with the usual measurement accuracy. The situation becomes completely absurd when not only the influence of one parameter, but - as usual - a whole range is required (window size, type of window, proportion of frame, shading, curtains, wall color, wall insulation, wall storage capacity, roof insulation, Roof ventilation, roof storage capacity, size of the inner wall, structure of the inner walls, color of the inner surfaces, permeability to joints, …). Each influence can also be changed continuously: the solar absorption coefficient of the outer wall from 0.2 to 0.8. Wishing to deal with all of these questions on the basis of field measurements with the above-mentioned measurement accuracy requirements would go beyond the budget of any research institute.
The questions mentioned are thus typical examples of tasks that can be solved with the help of thermal building models (usually EDP-supported)
- considerably faster (an annual simulation run per building variant costs a few secaonds computing time (in 2020; in 1994 it was approx. 1 h))
- in greater variety and
- with better accuracy and reliability
as with direct field measurements. The last point may be surprising, so here is a brief explanation:
Of course, simulations are only more accurate and reliable if the underlying model has been sufficiently validated. How this can be done will be explained later.
With a validated model, the unchanged parameters and boundary conditions in the treatment of every question can be kept exactly the same (“ceteris paribus”), which is precisely the great difficulty with every field measurement. Even unimportant influencing parameters can therefore be extracted from the noise of difficult to control but important influencing variables with the simulation.
Now there may be an objection that there is no interest in the effects of “such small” influences if they are lost in the noise of the main parameters. This objection is not valid for two reasons:
- The accumulation of some of the individually small influences results in noteworthy changes in building behavior (e.g. the “low energy house” type has approx. 70% less heating heat consumption compared to the type “Swedish building standard 1980” developed from cumulative “small” changes).
- In a large group (e.g. of some hundreds of buildings) the small savings of perhaps 5%, which are hidden in individual cases by other parameter influences, emerge significantly from the noise.
The first reason shows a way for the metrological validation of the models: large differences in cumulative changes can be reliably monitored. However, this does not relieve the need to determine the individual changes, otherwise it could be that a particularly expensive “improvement measure” has no big effect.
The second reason also shows a basic way for a validation: the measurement in very large samples, in which accidental influences such as different indoor climates average out. To do this, however, the buildings must be sufficiently identical in their entirety - which also means high expenditure. In Sweden (Täby [Blomsterberg 1990], Valdemarsrö [Lange 1990], Taberg [Fredlund 1989]) such measurements were actually carried out in settlements with more than 18 similar residential units. - It is clear that this method is also hardly suitable for answering the multitude of questions - after all, some of the model validations carried out stem from this work.
From the considerations so far it follows quite clearly:
| The method of choice for answering typical questions of structural influences on the indoor climate and heating energy consumption is the use of thermal computer aided building models. - On the other hand, validation of such models thus becomes one of the most urgent tasks of research. |
In practice, this finding has long since become established: Computer-aided thermal-technical building simulation is a widely used instrument. Of course, this does not say much about the suitability and accuracy of such procedures. A big part of the validation work has been done in recent research projects especially involving passive houses [Johnston 2020].
References
[Blomsterberg 1990] Blomsterberg, Å.: Ventilation and airtightness in lowrise residential buildings; Byggforskningsrådet, Stockholm D10:1990
[Feist 1994] Thermische Gebäudesimulation; 1. Auflage, 366 Seiten, 1994
Thermal building simulation, first edition,1994 (in German)
[Fredlund 1989] Fredlund, B.: Blocks of flats with glazed verandas, Taberg; Swedish Coun¬cil for Building Research, Stockholm D3:1989
[Johnston 2020] Johnston, D. et al: Are the energy savings of the passive house standard reliable? A review of the as-built thermal and space heating performance of passive house dwellings from 1990 to 2018. March 2020, Energy Efficiency, DOI: 10.1007/s12053-020-09855-7
[Lange 1990] Lange, E.: Radhus i Valdemarsro, Malmö - En energi- och innklimatanalys, Byggforskningsrådet. Stockholm R1:1990