Table of Contents
Efficiency vs. Efficiency Factor
It is often mistakenly thought that “efficiency” is synonymous with the efficiency factor. This is only true if both quantities on the right of the equation
efficiency = benefit / effort
have the dimension of “energy” or “power”. But very often the provided benefit has nothing to do with energy. For example, the benefit can be a mileage (unit “miles”). For example, the effort can be the fuel required (unit “gallons”) and the efficiency of this service will be given as
mileage / (fuel consumption)
Measured in “miles/gallon”. In Europe the inverse value
effort coefficient = 1/efficiency
has become established, i.e. the specific fuel consumption in litres/(100 km).
- Such values characterising efficiency are not “efficiency factors” - they are values with a dimension.
- It is not possible to introduce an efficiency factor instead of this because most activities requiring the use of energy do not have the dimension of energy.
- And there is no “minimum amount of energy required based on physical reasons” for providing a benefit; the contrary assumption is also a widespread misconception – the “minimum amount of energy required” is zero in most cases (or an extremely small value greater than zero).
Is that a purely academic issue? No, not at all.
For example, the efficiency factor of heating boilers cannot be increased to more than 100% (law of energy conservation) and today values in the range of 90% have already been achieved. But still the efficiency of the heating application (e.g. heated space/heating energy) can be improved almost as far as you want by applying improved thermal protection. If only the efficiency factor was of importance, there would be no potential for saving a lot of energy with heating. Based on a broader understanding of this, it is evident that the required “heating demand” can be reduced to near zero by using better insulation, therefore there is a very great efficiency potential here. That this also works in practice, has been demonstrated by numerous Passive Houses that have been built and are now inhabited.
This also applies for many other energy applications; especially the final use of energy at the end of the supply chain provides a significant potential for better efficiency. For example:
- Heat storage tanks can be insulated more efficiently, thereby considerably reducing the energy consumption for maintaining the temperature (the thermos-flask principle).
- The same applies for heat distribution pipes (particularly domestic hot water and circulation pipes).
- Heat can be recovered from waste water from washing and showering.
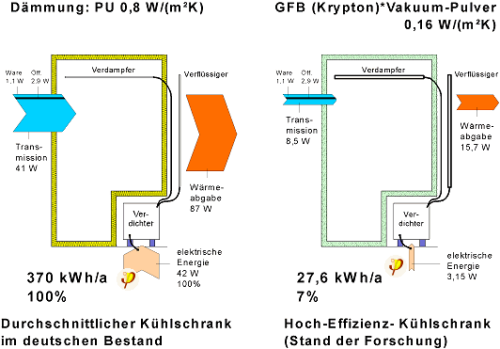
- Insulation which prevents heat losses is just as effective for cooling performance (see Fig 1).
- By using heat recovery, energy can also be used more efficiently for industrial processes. An example of that is a counter-flow firing kiln: (hot!) fired goods approach the as yet cold, unfired goods along the production lines.
- Improved efficiency of materials and recycling of energy-intensively produced materials can also reduce the energy consumption.
A consistent analysis of all services provided through the use of energy today shows that from the physics perspective, this mainly consists of maintaining a state of non-equilibrium. However, by intelligent process management, this can be transformed into an almost stable equilibrium state. An extremely small amount of energy is required for this. For example:
- Warm home: non-equilibrium state, “higher indoor temperature” in comparison with “cold surroundings”. Intelligent process management: all types of thermal protection. Practical example: Passive House.
- Climatised home: non-equilibrium state, “cool indoor temperature/lower humidity “in comparison with “hot surroundings/high humidity”. Intelligent process management: thermal protection, heat and moisture recovery. Practical example: Passive House with a compact unit.
- Cooling chain: non-equilibrium state, “cooler temperature in the cooling space” in contrast with “warmer surroundings/high humidity”. Intelligent process management: thermal protection. Practical example: vacuum-insulated cooling space.
- Transportation (see Fig 2): non-equilibrium state, ” movement with friction”. Intelligent process management: reduction in friction, recovery of braking energy. Practical example: Hypercar, 1.5 litre car.
Transportation efficiency: Different vehicles consume different amounts of fuel for the same service (transporting 1 person over a distance of 100 km):
→ 12 litres/100 km per person (a relatively old car)
→ 6 litres/100 km per person (an average modern car)
→ 3 litres/100 km per person (a modern efficient car)
→ 1 litre/100 km per person (prototype of the 1-litre car or “Hypercar”)
→ 0 litres/100 km per person (a frictionless vehicle on a brachistochrone curve; see Fig 2
 |
|
| Fig 2: An intriguing experiment: the body which follows the longer path through the trough reaches the end more quickly. No energy is required for this as long as the process is reversible. |
For those, who want to see the proof - it's at the end of this page
| Brachistochrone curve? Even Galilei knew about it: it’s the fastest path from A to B without using any energy in a homogeneous gravitational field. → Do you want to know more? Download the following article: "Wissenschaft, Kultur und Lebensart rund um das Passivhaus" (in German) which not only explains about the brachistochrone curve but also about exergy and anergy and why Galilei still hasn't managed to become fully established in daily life in contrast with Aristoteles. |
Conclusion
For most activities, energy is not required at all, or at least only a very small amount of energy is needed – but only when losses can be consistently avoided. This is because these activities do not have an energy dimension and in fact consist of maintaining a particular state.
Improved energy efficiency therefore can almost completely substitute the energy previously required. “Energy efficiency” is almost equivalent to a new energy source - but only almost, because energy efficiency is much better. Energy efficiency is clean, inexhaustible and free during the period of use. Energy efficiency can be applied everywhere. And: we ourselves can “produce” energy efficiency everywhere on the globe; it is integrated in smart products from the very beginning - for the benefit of the user (lower running costs and increased comfort), with advantages for the manufacturers (higher quality and therefore higher added value) and advantages for the national economy (domestic employment) and for the environment (climate protection).
There can only be winners - even the suppliers of conventional energy can be winners if an adequate time horizon is adopted: e.g. the supply of fuel oil will last much longer and can be sustained with lower risks if the efficiency of use is significantly improved.
Energy efficiency can be significantly improved in many areas, as can be seen in this analysis of the energy balance.
See also
Energy efficiency – the key to future energy supply
Appendix: Proof for statement in fig.2
We call the velocity on the horizontal path v0. This velocity has only a horizontal (x-)component which is constant according to Galilei's law (first Newtons law).
Now consider the body going through the trough. It starts with the same horizontal velocity. But it gains energy from the gravitational field, the energy conservation law gives for the total kinetic energy at a place x
1/2 m v(x)2 = 1/2 m v02 - m g z(x)
Here v(x) is the total velocity at place x and z(x) is the vertical coordinate of the lower body, z=0 is the hight of the plane. Note that z(x)<0 for all x>0 and x smaller as the goal coordinate. The additive energy term on the right side is therefore always positiv, energy is gained from the gravitational field at all places for the body on the lower lane. Thus, the total velocity v(x) is always higher than the velocity v0.
Now, as the body rides down the slope, kinetic energy in z-direction is transformed into kinetic energy in x-direction. How high wil the vx(x) be? See the vector diagramm in Fig. 2: The total velocity is tangential to the slope:
v(x)2=vx(x)2+vz(x)2
Thus, the kinetic energy in x-direction is beeing increased - therfore, not only v(x)>v0, but also vx(x) > v0 for all x on the downward slope. Time reverse symmetry gives, that at the upward slope all x-velocities are equal to the x-velocities at the same hight on the downward slope. This means, that at any point in the lower path the x-component of the velocity is higher than the x-velocity of the body on the plane. If sgoal is the horizontal distance of the goal, the time for the upper body will be
tupp = sgoal / v0
the time for the lower body, however, will be shorter, because it's x-velocity is always greater than the velocity of the upper body:
tBra = ∫1/vx(x) dx < ∫1/v0dx = sgoal / v0= tupp
q.e.d.