Table of Contents
Heated basement
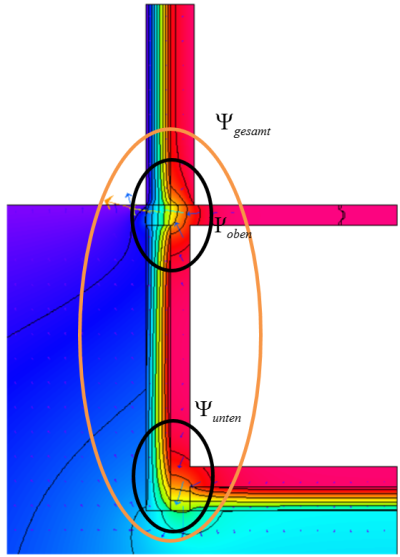
In the norms DIN EN ISO 13370 and DIN EN ISO 10211, only one Ψ-value is determined for a heated basement. This includes the upper connection of the basement ceiling and the connection of the basement wall to the basement floor slab. In the Ground worksheet of the PHPP it is sufficient to enter $\Psi_{total}$ (as a perimeter thermal bridge). Alternatively, both connections ($\Psi_{upper}$ und $\Psi_{lower}$) can be examined separately for the criterion relating to absence of thermal bridges.
The procedure for determining the mentioned linear thermal transmittance is given below. Here it should be mentioned that in the Ground worksheet of the PHPP, U-values for the basement floor slab and the basement wall are determined using the approximation function in the DIN EN ISO 13370, with consideration of the ground. In this way, Option A or Option B can also be applied for heated basements. In the context of certification for a construction system however, Option B should also be applied here for determining the Ψ-values.
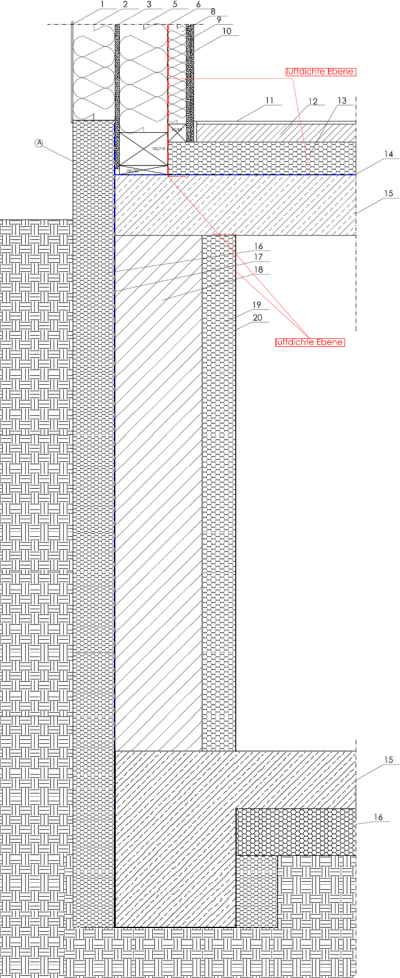
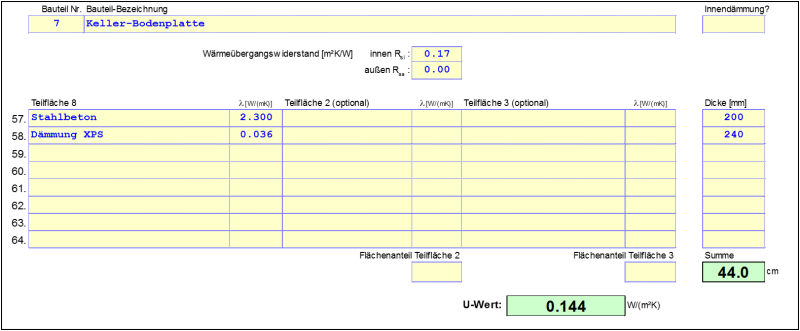
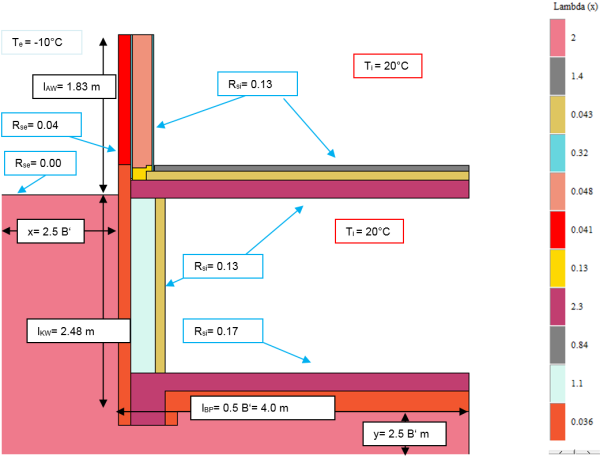
According to the figure above, the U-values of the building components that are relevant for determining the Ψ-value can be ascertained as follows:
Calculation models
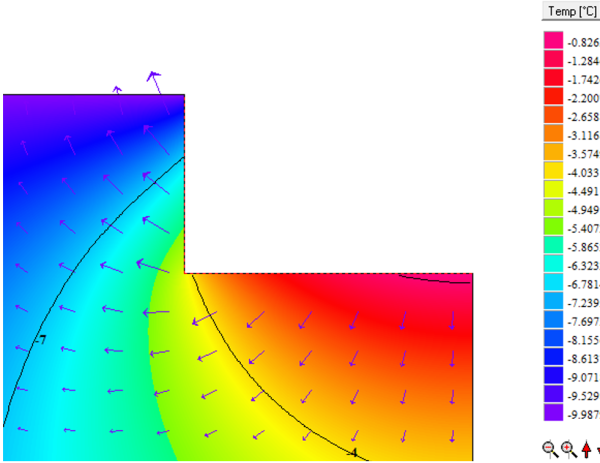
Calculating the conductance $L_{2d}$
$$ \large{\dot{q} = 38{,}123 \, \dfrac{\text{W}}{\text{m}}}\\ $$
$$ \large{L_{2d} = \dfrac{\dot{q}}{T_i-T_e} = \dfrac{38{,}123}{30} = 1{,}2708 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}} $$
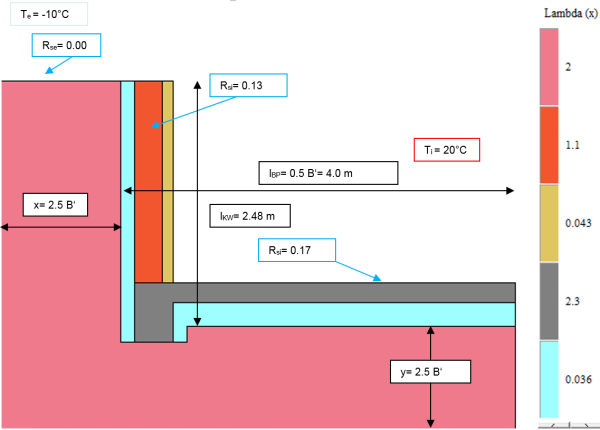
$L_{2d}$ is thus calculated. In order to be able to determine the Ψ-value, the conductances of the exterior wall, the basement wall and the basement floor slab must also be calculated. The conductance of the exterior wall can also be calculated easily here from the U-value and the adopted length. The conductance of the basement wall and the basement floor slab must be calculated in accordance with Option B, that is using an additional calculation. For this, the building components in contact with the ground are depicted by their transfer resistance in a manner similar to the floor slab.
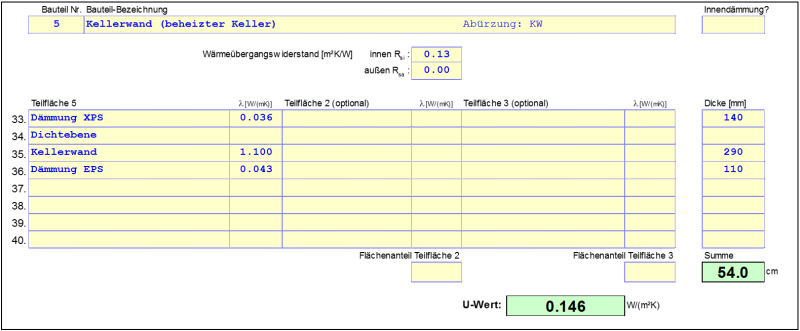
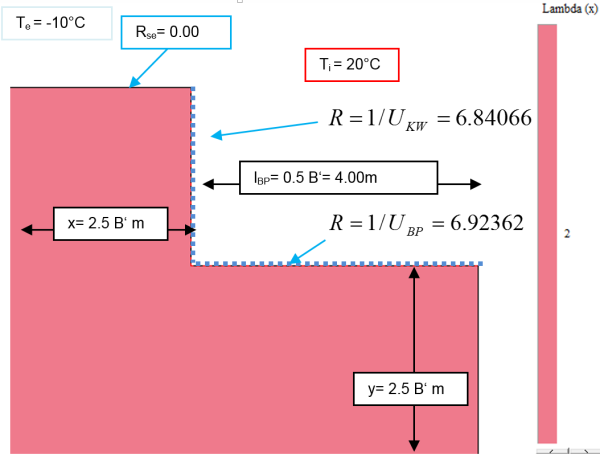
Conductance of the basement floor slab and the basement wall $L_{BP,KW}$
$$ \large{\dot{q} = 22{,}190 \, \dfrac{\text{W}}{\text{m}}}\\ $$
$$ \large{L_{BP,KW} = \dfrac{\dot{q}}{T_i-T_e} = \dfrac{22{,}190}{30} = 0{,}7397 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}} $$
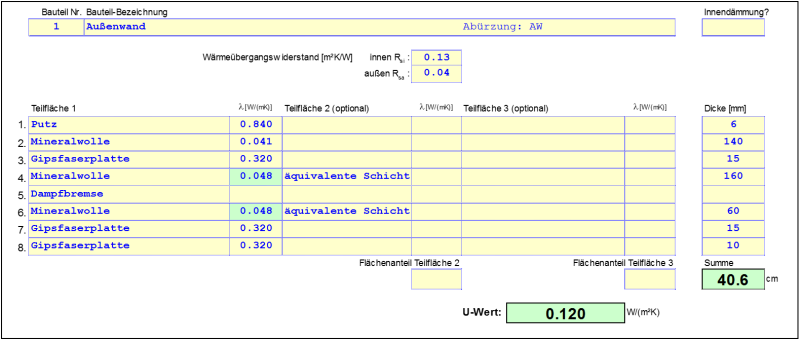
Calculating the conductance of the exterior wall $L_{AW}$
$$ \large{U_{AW} = 0{,}1205 \, \dfrac{\text{W}}{\text{m}^2 \cdot \text{K}}} $$
$$ \large{L_{AW} = l_{AW} \cdot U_{AW} = 1{,}83 \cdot 0{,}1205 = 0{,}2205 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}} $$
Determining the Ψ-value (overall)
$$ \Psi_{overall} = L_{2d}-L_{AW}-L_{BP,KW}=1{,}2708-0{,}2205-0{,}7397=0{,}311 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}} $$
In practice, pre-prepared Excel templates are used here also for determining the Ψ-values. The heat flows and necessary lengths can be entered here and the desired Ψ-value is received as the result directly:
Note: this is not a thermal bridge free connection. In the example given here it is relatively clear that the basement wall connection to the basement floor slab has not been implemented in an ideal manner. One would advise the client to install insulation under the foundation as well (see AkKP 35). Regardless of that, the question that arises is, what about the upper connection? Can the floor/ceiling connection be regarded as thermal bridge free? Strictly speaking, one cannot consider both these connections separately from each other. The ground represents a thermal connection between the basement wall and the floor slab. Heat flow through the floor slab thus influences the heat transfer through the basement wall and vice versa. In most cases however, the basement wall to exterior wall connection is near or even above ground level. For this reason there are less interactions, and separate specification of $\Psi_{lower}$ and $\Psi_{upper }$, which is desirable in practical application, is justified. We suggest that first the lower connection should be calculated uniformly. The opposite is also possible; the consequence would be a (usually only slightly) different allocation of $\Psi_{overall}$ to $\Psi_{lower}$ and $\Psi_{upper }$.
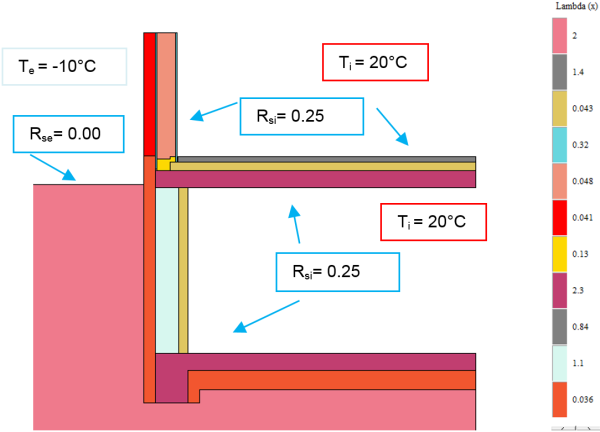
Determining the conductance $L_{2d}$
$$ \Large{\dot{q} = 29{,}588 \, \dfrac{\text{W}}{\text{m}}} \\ $$
$$ \large{L_{2d} = \dfrac{\dot{q}}{T_i-T_e} = \dfrac{29{,}588}{30} = 0{,}9863 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}} $$
The conductance $L_{BP,KW}$ is already known from the overall calculation. The following Ψ-value results for the basement wall connection to the floor slab:
Ψ-value calculation (lower connection)
$$ \large{\Psi_{lower} = L_{2d}-L_{BP,KW}=0{,}9863-0{,}7397 = 0{,}247 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}} $$
The Ψ-value for the upper connection can now be calculated from the difference between $\Psi_{overall}$ and $\Psi_{lower}$. The influence of the lower connection is thus included in $\Psi_{upper }$.
Ψ-value calculation (upper connection)
$$ \large{\Psi_{upper} = \Psi_{overall}-\Psi_{lower} = 0{,}311-0{,}247 = 0{,}064 \, \frac{\text{W}}{\text{m} \cdot \text{K}}} $$
The basement ceiling connection isn't free of thermal bridges either.
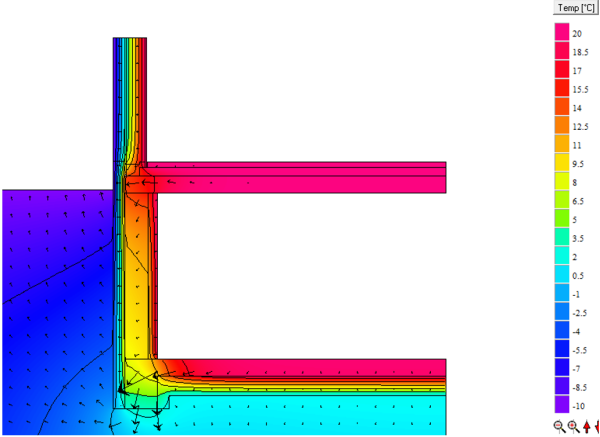
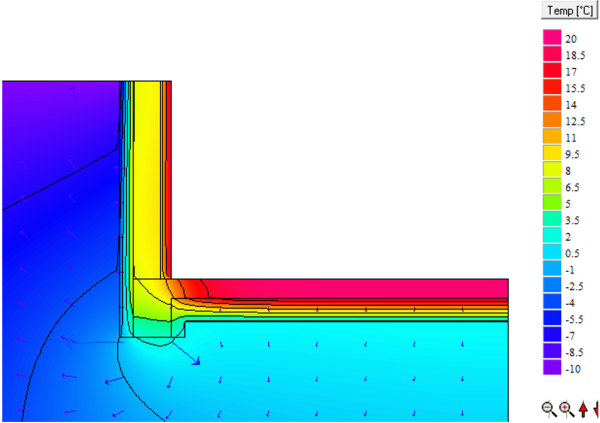
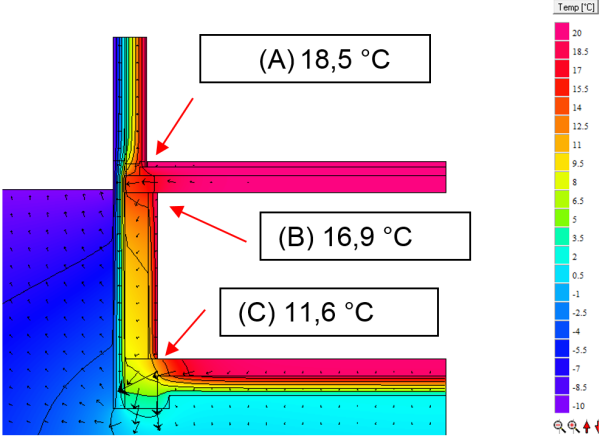
Determining the surface temperature
For determining the minimum surface temperature and the $f_{Rsi}$ factor, the same procedure can be used in this case as for any other thermal bridge.
Determining the minimum surface temperature $f_{Rsi}$
$$ \large{f_{Rsi,A} = \dfrac{18{,}5-(-10)}{20-(-10)} = 0{,}94} $$
$$ \large{f_{Rsi,B} = \dfrac{16{,}9-(-10)}{20-(-10)} = 0{,}89} $$
$$ \large{f_{Rsi,C} = \dfrac{11{,}6-(-10)}{20-(-10)} = 0{,}72} $$
Note! areas which are near the ground surface are subject to bigger temperature fluctuations than those which are further away from the surface. The steady-state calculated surface temperatures of areas further away are therefore less meaningful, but are usually on the safe side because in reality the boundary conditions necessary for this would have had to prevail for months. If more exact surface temperatures are required, then the solution may lie in two or three-dimensional transient calculations.