Table of Contents
Insulation works – Evidence no.1 "Measurements at a highly insulated wall"
Long-term measurements at exterior walls of highly insulated new buildings
Thermal protection works - Solid evidence has been provided by real-life measurements.
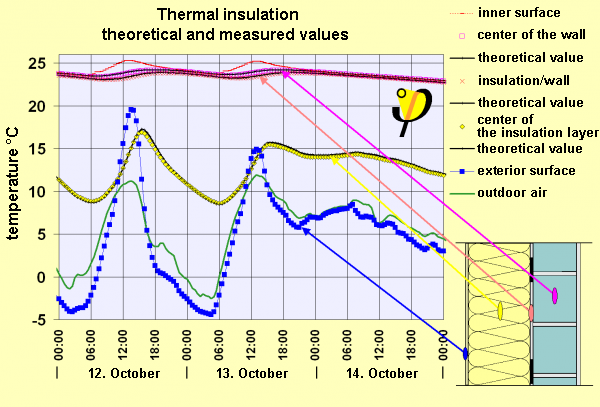
The following image shows the temperatures measured by high-precision sensors built into the surfaces and the structure of very well insulated walls. The cross-sectional view of the wall is shown in the bottom right corner of the image. The left side of the cross section is the exterior side of the wall. The load carrying structure consists of a 175 mm lime sand brick wall (grayish blue). A 275 mm insulation layer has been added to the exterior of the wall and plastered on the outside.
Temperature sensors have been fitted:
- just below the inner surface of the interior plaster (red dash line)
- in the center of the brickwork (purple square)
- in between the insulation layer and the brickwork (light red cross)
- inside the insulation layer (12 cm below the outer surface, yellow diamond)
- just below the outer surface of the exterior plaster (blue square)
- outdoor air (green curve).
Each sensor measures the temperature with an accuracy of ±0.15 °C. An electronic data acquisition device has recorded the measured values at an interval of 30 minutes over the course of several years.
The diagram shows the values measured over a period of three consecutive days. The time segment can be chosen at random. The segment shown here is interesting as it shows a period with some significant temperature changes.
Analysing the measurement results
The measurement results clearly indicate that the heat insulation works:
- Throughout the entire period of time outdoor air temperatures are well below the room temperature: Outdoor temperatures vary between -2.5 und 11.9 °C, with a mean temperature of 5.6 °C.
- Room temperatures mostly correspond with those measured at the internal wall surfaces. These temperatures are between 22.9 and 25.3 °C (nice and warm!); the mean temperature is 24 °C. Note that the heating system was not turned on in this room throughout the entire period of time. The heat is provided exclusively by the sun entering through the windows facing south.
Despite the significant differences between indoor and outdoor temperatures of 18.4 degrees on average the bricks never turn cold. Instead these remain at an almost constant comfortable temperature close to that of the room air. Extremely little heat is lost through the wall and can be compensated for by the solar energy gained through the windows in the room. This clearly proves: Insulation works.
The line of reasoning continues by taking a closer look at the temperatures measured inside the brick part of the wall itself. In the image, these values are represented by three curves which are relatively close together: inside the internal layer of plaster (top curve), in the center of the brick wall, and on the outside of the wall (in between the layer of polystyrene and the wall):
Very low heat flows
Since all three temperature curves are very close together we can see that little heat escapes from the exterior surface of the brick wall: If that were the case the exterior of the brick would be a lot colder than the center of the brick and even more so than the interior surface. Yet, the temperature measured at the exterior of the brick is hardly below that of the interior plaster: at an average of 23.4 degrees Celsius on the outside and 24.1 degrees on the inside.
These findings can even be used for a rough estimation of quantitative results: The mean temperature decrease in the brick part, including the layer of interior plaster, amounts to 0.63 degrees, and to 19.4 degrees between the exterior surface of the brick wall and the external plaster on the insulation layer. This means that the insulating effect provided by the insulation layer is increased by a factor of 19.4/0.63 ≈ 31 compared with that of the brick wall. This result is even better than the theoretical value of approx. 28.5 resulting from a simple U-value calculation: In building physics, the “insulating effect“ is defined as the thermal resistance of a building component resulting from its thickness divided by its thermal conductivity. The factor of 31 is deliberately called a “rough estimate” and would only be obtained precisely if the temperatures inside the components were exactly identical at the beginning and end of the time period. However, this is not the case. More exact calculation results will only be obtained by looking at a much longer timeframe. In that case, a variation in temperature at the beginning and end of the period would play a minor role.
In any case, this rough analysis provides further evidence: Insulation works very well; very little heat flows through the insulation layer; the insulating effect of the wall construction is increased many times over by the insulation layer.
Transient effects
Unfortunately, the rough estimation described under very low heat flows does not take into account transient effects. This is only acceptable for measurements carried out over a very long period of time – three days are not enough. This problem can be solved using methods established in buildings physics: The calculation based on the transient heat conduction equation (also known as Fourier’s differential equation) will produce completely correct results. We are – and have always been – using this precise calculation method for all scientific analyses.
The calculated results based on the transient heat conduction equation are already included in the diagram above (!): represented by the continuous black curves, each very close to the measured values. In fact, they run so close to the measured values making it difficult to tell them apart. To see the differences, just click on the diagram to download a version with higher resolution. It will reveal a maximum variation of approximately 0.25 degrees Celsius for the temperature measured insight the insulation layer on 12 October at 3:30pm. This variation is negligible as it remains within the accuracy limits typical for such measurements.
Comparing the theoretical calculation values (black curves) and the actual measurement results (coloured symbols) obtained for this wall construction proves: Both theoretical and experimental approaches provide the same results. This creates great confidence in the calculation methods.
The detailed comparison of measured and calculated values taking into account transient effects leaves no doubt: Insulation works. And it fully lives up to the expectation raised by the calculation methods of building physics: Among its many advantages it saves a great amount of energy for heating.
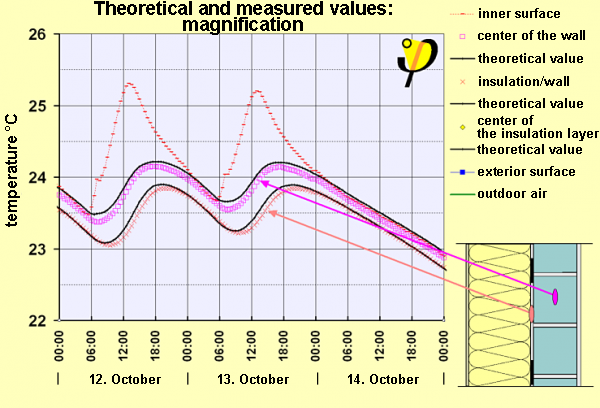
Magnified view
This magnified version of the graph clearly shows the temperature changes in the brick wall (the time period is exactly the same). Please note the high resolution of the temperature curves: The difference between the continuous and the horizontal broken lines is 0.5 degrees Celsius. This graph shows variations as small as 0.1 degrees or less. This view confirms just how well the calculated values (clack curves) match the measurement results (coloured symbols).
This magnified view illustrates both the fact and the reason for temperature changes within the brick wall. The change in temperature does not occur due to heat flowing from the wall to the exterior – after all, this is where the insulation layer does an excellent job of shielding the wall from the environment. It mostly occurs at the internal wall surfaces (red lines -): This is where the temperature changes are greatest and where they occur first. This can be explained quite simply (data from 12 October):
- First, between 12am and just before 6am, the temperature decreases in all brick layers of the wall: The wall gives off heat (to the interior and exterior). Inside, the heat is radiated towards the window surfaces which have cooled down during the night.
- From 6am on, solar radiation through the windows increases (12 October was a clear day). All internal surfaces, including the interior wall surfaces, are heated by the sun. The wall on the west side of the building is even directly hit by the sun until 9am, hence the rapid increase (at 7:30 the window frame causes a shadow; the same happens on 13 October). Later on, radiation occurs only indirectly by heat radiating from the floor which is now directly hit by the sun. Yet, even then the temperature at the internal surface continues to increase and peaks at 25.3 degrees Celsius at 1pm.
- This rapid increase in temperature is passed on to the next layer fitted with a sensor, 88 mm below the surface. However, this increase occurs with a certain delay and at a lesser rate: The temperature “only” increases by 0.75 degrees and only peaks at 6pm.
- The most outward layer of the brick wall only reaches its maximum temperature at 7pm and doesn’t exceed 23.8 degrees Celsius. At this level, there is also some influence from the exterior which is largely reduced by the thermal insulation but is noticeable nevertheless. This is mostly due to the fact that the temperatures on the outside of the brick wall are always below those at the internal surfaces.
This high resolution diagram clearly shows that the rather rapid changes start at the interior of the construction. However, the main direction of the heat flow in the wall is outward; the temperature sequence is almost always as follows: internal surface, center, outside. The average remaining temperature differences are very small (approx. 0.6 degrees Celsius at the brick wall); the remaining heat loss is therefore rather insignificant. This high resolution view proves just how well the calculations match the measured values.
Conclusion
The measurement results from the insulated wall provides clear evidence that:1)
- Heat insulation works as desired reducing heat losses to a great extent – in this case by a factor of 28.
- This insulation effect corresponds exactly with the generally accepted rules of building physics.
The correspondence between theoretical calculations and practical results has been proven many times in measurements. The present author has no notice of a single scientific publication reporting on a discrepancy between theoretical and measurement results that haven’t been accounted for.
The effectiveness of good heat insulation can also be illustrated by putting together several exterior building components to make up a small “house“. In the spring of 2007 “ice block bets” took place in several German cities. A block of ice is stored in a highly insulated house and gradually melts as heat enters the building. Even experts are often surprised at just how long the ice lasts with good insulation.
See also
In natural sciences a “proof“ calls for much stricter criteria than those required in general practice. According to these criteria a proof in the strict sense of the term can only be provided in mathematics, and only based on so far unproven propositions (so called axioms). In mathematics these axioms are simply assumed to be true.
In natural sciences, however, such assumptions are not possible as they focus on achieving maximum agreement with real-life observations. Basic laws such as the law of thermal conduction cannot be proven: Proving their validity would require verifying all possible cases. Therefore, all scientific “laws” will continuously be subject to verification based on new experiments. This is the main characteristic of serious science and the basis for both scientific progress as well as the great reliability of the current state of scientific knowledge. So far it has stood any test. The state of scientific knowledge is still not to be considered the “absolute truth”, but it provides the best possible description of specific phenomena.
It is not “absolutely“ certain, and even less provable, that the heat conduction equation provides a correct description for the thermal processes in building components. It is only about as certain as the assumption that the earth rotates around the sun. This is an idea which was very difficult for people to accept in the beginning, yet today it is considered an undoubted truth.
By the way: Scientists have been carrying out experiments to verify the heat conduction equation for over a century, some of the early ones much more tricky than today’s. Today, the equation is used to calculate the temperature curves in power units or in nuclear reactors. If the results weren’t reliable, the consequences could be disastrous. Even simple developments such as the insulation of refrigerators or pipes, thermos flasks or covers for eggs and tea mugs, or even blankets are based on this basic law of heat conduction.