Table of Contents
PB 41: Planning tools for the summer situation in non-residential buildings
Dr. Jürgen Schnieders, Passivhaus Institut, Rheinstraße 44/46, 64283 Darmstadt
1 Introduction
The summer behaviour of non-residential buildings often plays an important role when planning these, because the boundary conditions that are relevant for the summer can differ significantly from those in residential buildings. Sometimes concentrated internal heat loads may occur during certain times, for example in classrooms or conference rooms. Occasionally, due to higher occupancy density and greater technologisation, these internal loads may be considerably higher than those in residential buildings. Added to this is the tendency to use large glazing areas for utilising daylight and also for aesthetic reasons. These result in accordingly higher solar gains. In some circumstances, a dress code may also apply in non-residential buildings which, in case of moderately high temperatures, may lead to exceeding of the comfortable range.
Questions, such as whether thermal comfort in summer is adequate even without active cooling, or how high the energy demand for space cooling is, and how high the output of the cooling system must be, are therefore particularly relevant when planning non-residential buildings. In principle, it is always possible to carry out a dynamic thermal building simulation for assessing the summer conditions. With careful data acquisition and application of suitable models, this can predict the thermal conditions inside the building with a high degree of accuracy. However, not all building simulation programmes depict the relevant heat transfer processes sufficiently accurately; usually the performed calculations are barely verifiable and the effort for a substantiated and meaningful simulation is high. For example, in order to obtain results that justify the effort for a simulation, it is generally also necessary to include the adjacent zones besides the thermal zones that are of actual interest. (See also Section 3.4).
The following article will therefore deal with the validity of simplified algorithms as already implemented in the Passive House Planning Package [PHPP] for non-residential buildings currently. It is obvious that there are limitations for such simplified methods; it is essential to be aware of the limits of this application. The focus of this article is on usage as offices or seminar rooms since, for one thing, this type of usage is very common, and for another, the differences from residential buildings as mentioned above are already relatively distinct.
The article will first consider the case of active cooling. Of central interest here are the calculation of the annual useful energy demand for space cooling (hereafter referred to as useful cooling), and the cooling load. In the second part, calculation of the frequency of overheating, i.e. the number of hours in a year where the indoor temperature exceeds 25°C in passively cooled buildings, will be examined in more detail for non-residential buildings.
Verification of the simplified algorithms in the PHPP will take place based on the simulations using the dynamic thermal building simulation software DYNBIL, which has been validated for residential and office use based on measurements in inhabited buildings. The algorithms in the DYNBIL program are so close to physical principles that we consider the results to be valid for other types of usage.
The calculations will take place using the same simulation model which was used for the article on concrete core temperature control by Wolfgang Hasper in this Protocol Volume. The room being studied can be situated in the centre of one side of the building or at the corner; accordingly it has windows on one or two sides, either with a moderate window ratio of 40% of the respective facade, or as full glazing. Different levels of insulation can also be considered, based on the Passive House standard or the currently valid EnEV standard for new buildings. Important note: the windows in the following examined cases are without exterior shading, so that high solar loads can also be depicted. In part, a variant without windows will be examined in order to allow depiction of the behaviour of buildings with effective exterior shading attachments, e.g. venetian blinds in front of triple low-e glazing.
2 Active cooling
2.1 Prologue: heating
Dynamic simulations calculate the thermal conditions in the building in time steps which are usually much less than one hour. Heat transfer processes in building components and the room are shown in detail. In contrast with this, there are energy balancing methods such as the annual and monthly method used in the PHPP or the DIN V 18599, which calculates the heating balance by means of a specified balance boundary over longer periods of time using the law of conservation of energy. Energy balancing methods have significant advantages in terms of application, computation time and interpretability, whereby the results for the heating demand of typical residential and non-residential buildings correspond very well with the dynamic simulation.
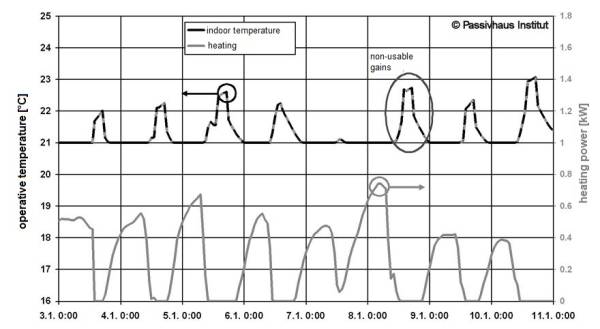
In the energy balance method, heat gains and heat losses are ascertained separately using a fixed balance limit and then added together. Dynamic effects are taken into account by means of a mathematical strategy which uses the so-called utilisation factor for free heat in the building. On observing Figure 1, the underlying problem becomes apparent: internal and solar heat gains can become so high that in certain phases of the heating period, heating is no longer necessary. The share of heat gains in excess of the heat losses then results in operative temperatures exceeding the setpoint temperature (here: 21°C). The average indoor temperature during the balance period, which is actually required for determining the heat losses, is thus not the same as the setpoint temperature and not known at all in the first place.
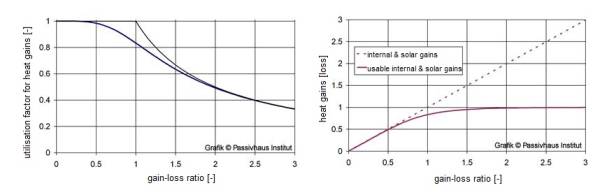
In the energy balance method, this problem is solved by introducing the utilisation factor. Only part of the internal and solar heat gains is actually effective for reducing the heating demand. What is important is that this share can be calculated easily with sufficient accuracy using the ratio of heat gains to heat losses and the thermal inertia of the building. This dependence is shown in Figure 2. Details regarding the determination of the utilisation factor are given in [Feist 1998a].
The monthly method in the PHPP uses the utilisation factors in accordance with [EN 13790]. Experience with this calculation method for residential buildings has been excellent compared with the dynamic building simulation (for example, see [Feist 1998]), and it also proved successful for inhabited buildings as well as in the direct probation of inhabited buildings.
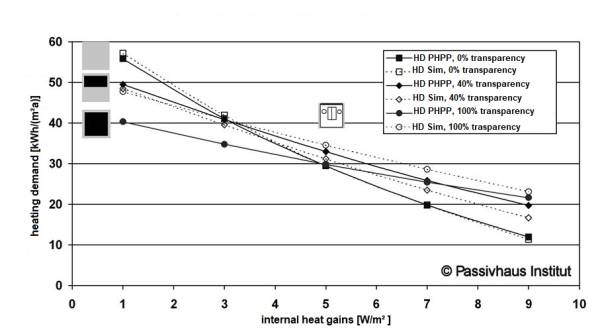
Two examples provide more information regarding the scope of application of this method. Figure 3 shows the calculated heating demand for the central room of the simulation model with a window on one side and insulation to the EnEV standard, calculated with consistent indoor conditions with various levels of internal gains and window area ratios. The calculation was carried out using the PHPP as well as the dynamic model in DYNBIL as the comparison standard. For the case without windows, it can be seen that there is excellent correlation between the simulation and energy balance method for all values for internal heat gains. The gradients only diverge noticeably in the case of larger window areas and extra high internal heat gains.
Principally, the results are similar in the second case with the Passive House corner room with windows in both exterior walls (Figure 4). Both calculation methods correlate very well if there are no windows areas or if window areas are moderate. The results no longer correlate well only in the case with full glazing; the simulation yields significantly higher heating demand values. The difference is greatest for low internal heat gains where it is just 5 kWh/(m²a). This variation is certainly due in part to the fact that the solar gains are ca. 125 kWh/(m²a) with this configuration, of which 13 % are reflected back in the simulation model, while this type of geometrical effect is not specifically taken into account in the PHPP. The difference in the solar supply alone is thus already greater than 15 kWh/(m²a).
However, all calculation methods have limitations in cases with such high heat gains. If we consider the indoor temperatures reached in the case with the greatest difference (internal heat gains 1 W/m², Figure 5), it becomes apparent that temperatures much higher than 30°C may be reached even on sunny days in February. This would certainly be unacceptable for users. If the upper limit for the indoor temperature is set to 25°C, whether by means of active cooling or through natural window ventilation, then some of the solar gains will be removed again directly, and heating will again become necessary at an even earlier time. This would increase the heating demand additionally by almost 5 kWh/(m²a) compared with the “unsophisticated” simulation without limitation of the temperature. The relevant points are also depicted in Figure 4.
As shown in the example, the heating demand for buildings with such high solar gains can only be determined with some degree of uncertainty, which is also due to the uncertainties regarding the available solar irradiation (back reflection or radiation transfer towards the outside through the second window, influence of shading elements outside the building) in addition to an upper limit for the temperature. Such a design generally appears to be less advisable on account of the higher heat flows.
Altogether, in the energy balance method, the utilisation factor appears to have been calculated a little too low with constantly free heat (i.e. dominating constant IHG), and a little too high with temporally concentrated free heat. Thus, in typical cases both influences balance each other out and the heating demand according to the PHPP correlates with the simulation.
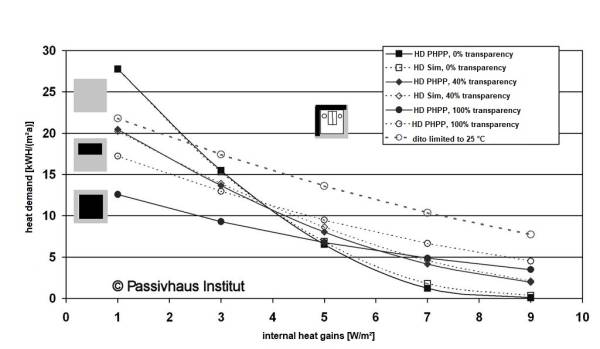 | 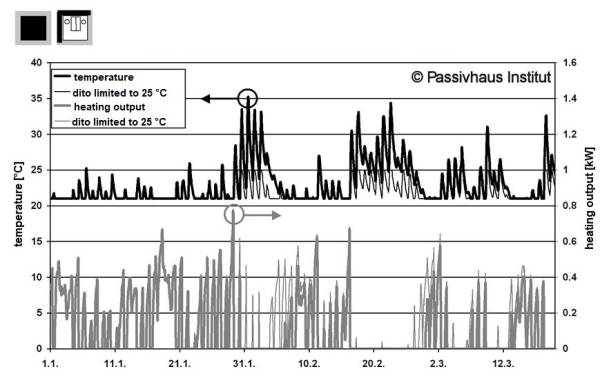 |
| Figure 4: Comparison of the calculated heating demand for the corner office in the Passive House standard according to the simulation and the PHPP | Figure 5: Temperature curve and heating output for the fully glazed situation with low internal heat gains from Figure 4. This figure shows the standard case where the indoor temperatures may increase without limitation, and the case where the indoor temperature is limited to 25°C. |
2.2 Useful cooling demand
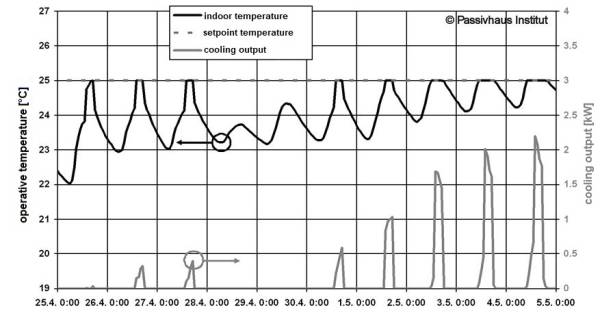
The principle of energy balancing using a utilisation factor works not only for heating but also for cooling. In the Central European climate, periods requiring cooling, as well as periods without a cooling demand, arise on many days during the summer. Figure 6 illustrates this situation.
Analogous to the winter case, an energy balance can also be prepared for this. Here, the opposite takes place: the cooling system works against the solar and internal heat gains, the transmission and ventilation losses provide additional support for the cooling system (in Central Europe the average monthly temperature is always much less than 25°C, in contrast with warmer climates there are no transmission or ventilation loads). Since losses also occur if cooling does not take place, a utilisation factor has to be determined for the losses. This is done according to the same principle as for heat gains in the heating situation.
In contrast with winter, the solar heat gains through the roof and walls in summer play a significant role. The exterior surface of a dark-coloured roof can easily reach temperatures of 70°C through solar incidence. Depending on the standard of thermal protection, a larger or smaller share of the solar energy absorbed here enters the room; the g-value of uninsulated building components can even be 10 %. The radiation gains and losses of the exterior surfaces in the summer must therefore be taken into account in the energy balance. This is the case with the PHPP.
Another important influencing parameter is additional ventilation during the summer. In Passive House residential buildings without active cooling, the summer temperatures could easily reach 40°C unless surplus heat is disposed of through opening of windows, as is normally done in practice. The PHPP takes into account summer cooling through the window ventilation method.
Seen as a whole, the energy balancing method for ascertaining the useful cooling demand works very well. Comparative calculations showed a good correlation between dynamic simulation and the PHPP for residential buildings in various climates, with and without summer ventilation, for lightweight and solid constructions.
 |  |
| Figure 7: Comparison of the calculated useful cooling demand for a centre office to the EnEV standard, according to the simulation and the PHPP | Figure 8: Comparison of the calculated useful cooling demand for a corner office to the Passive House standard according to the simulation and the PHPP |
As Figures 7 and 8 show, this also applies for non-residential buildings. In the case of insulation according to the EnEV or the Passive House standard as well as various internal heat loads and window area ratios between 0 and 100 %, the differences between the simulation and the energy balance method are within a few percent. As for the winter case, the greatest differences exist for the fully-glazed corner office. Again, at least part of the variation in this case can be ascribed to back reflections which have not been taken into account in the PHPP.
Office usage, i.e. temporally variable internal heat loads, has been assumed in Figure 8. The limitations of this method are most likely to be seen where the temporal variability of use increases, and where, if applicable, fluctuating temperature requirements arise and the average loads become greater.
Based on Figure 9, utilisation as a seminar room was therefore considered in addition. Internal heat loads of 25 W/m² prevail from Monday till Friday afternoon, during the highest outdoor temperatures, which equates to average internal loads of 3 W/m². A temperature requirement arises only during these times; outside of the usage periods, the temperature in the room can be set freely. The window areas are reasonably dimensioned; active cooling is augmented through intensive ventilation with an air change rate of 5 h-1 during the summer.
 |  |
| Figure 9: Temperature curve for seminar room usage with intensive nighttime ventilation and respective cooling output | Figure 10: Comparison of the calculated useful cooling demand for a centre office to the Passive House standard with seminar room use according to the simulation and the PHPP |
As can be seen in Figure 10, the energy balance method functions perfectly well even in this situation. This is astounding, given the fact that information regarding temporal distribution of the internal loads is not available in the PHPP at all. The limitations of this method are reached when the internal loads are increased once more by a factor of 3, which is not unrealistic in the case of rooms with high occupancy densities. The results are now divergent. With such fluctuating loads, the effect of summer ventilation also is no longer depicted accurately.
2.3 Cooling load
The usual cooling load calculation based on the VDI (German Engineers Association) regulations for cooling loads (VDI 2078) takes into account the hourly values, and is carried out over two days with different solar altitudes. A much simpler method designed especially for Passive Houses is implemented in the PHPP. This requires that the summer heat loads in the Passive House are also minimised before active cooling can take place, for example by means of effective temporary shading fixtures. The basic assumption is that in this way, the heat loads arising during the course of a day can be stored in the building mass so that it will be enough to take into account the daily mean values for the cooling load.
The boundary conditions of the PHPP method are determined from a test reference year; the highest occurring daily mean temperature is combined with the highest value for solar incidence on the 30 warmest days. Added to this is a safety margin of 1 W/m² for the internal heat gains. For Passive House residential buildings, this method overestimates the daily mean cooling loads calculated by means of dynamic simulation, typically by about 2 to 3 3 W/m², since for one thing, the design day for a typical year is rather pessimistically selected, and for another, capacitative effects, which may play a role especially in the case of small cooling loads and solid buildings, are disregarded (the heat loads on the cooling load day will only arise on this day, so the building mass can also absorb some of these loads).
Figures 11 to 13 show examples with the daily and hourly mean cooling loads for non-residential buildings based on dynamic simulation and the daily mean value according to the PHPP plotted against the internal heat loads and window area. As mentioned before, movable shading fixtures have purposely been disregarded for the calculations carried out here; some of the cooling loads are therefore very high. The internal heat gains are assumed to be constant.
Basically, the conditions described previously for residential buildings are also found here. As might be expected, the hourly mean cooling load is usually much higher than the daily mean value, typically by a factor of 2. The daily mean cooling loads are systematically overestimated in the PHPP method, whereby the figure is independent of the amount of internal heat gains. There is an obvious dependence of the difference with reference to the window area (see Figure 14): the differences between the simulation and the PHPP are greater with larger windows. This is explained by the simplifications in the calculation method as mentioned. Basically, this dependence is not necessarily undesirable; large window areas lead to greater fluctuations in the solar loads; daily buffering reaches its limits even earlier due to this. If there are no windows, or if windows are well-shaded, then even the hourly mean cooling loads based on the simulation can be smaller than the daily mean values determined by the PHPP (see Figure 11 for small internal heat gains). Disregarding the heat capacity is particularly noticeable here.
The extent to which the reliability of this method covers even extreme weather conditions was examined using the data for the extreme summer of the German test reference years [DWD 2004]. The results calculated using the dynamic simulation are also shown in Figure 14. One can see that the cooling loads in the extreme summer are hardly any higher; the differences are mainly due to small window areas. The cooling load is determined primarily by the solar incidence and not by outdoor temperatures. The daily mean cooling loads determined by the PHPP are not only much higher than those determined in the simulation for the standard year, but almost more than those for the extreme year.
According to these results, the cooling load method of the PHPP is suitable for buildings with minimised loads, i.e. a good level of solar protection and internal loads that are either small or uniformly distributed in time. In these cases it provides enough reliability to compensate for some of the temperature fluctuations occurring during the course of the day. If loads are so high that daily buffering is no longer possible, then a method with higher time resolution will have to be used.
 |  |
| Figure 11: Cooling load plotted against the internal heat load according to different calculation methods - without windows | Figure 12: Cooling load plotted against the internal heat load according to different calculation methods - ribbon window facade |
 |  |
| Figure 13: Cooling load plotted against the internal heat load according to different calculation methods - fully glazed facade | Figure 14: Cooling load plotted against the internal heat load according to different calculation methods. Here the daily mean values from Figures 11 to 13 are summarised supplemented with the results of the simulation for the extreme summer |
3 Frequency of overheating
In the Central European climate, sensibly planned residential buildings as well as many non-residential buildings do not require active cooling. In such cases it is usually acceptable if the temperatures are temporarily just above the comfortable range. The frequency of overheating, i.e. the percentage of hours in a year which exceed a certain limit value, was introduced as a measure of summer thermal comfort in passively cooled buildings. In the PHPP this frequency of overheating is always based on a temperature limit of 25°C, unlike the DIN 4108. A value of 10% is still acceptable, but 5% is preferable. These limit values may appear to be high but are justified by the fact that normally, if the frequency of overheating is not too high, a large part of the overheating hours have a temperature between 25°C and 26°C, so that the periods of perceptible discomfort are considerably shorter.
Basically, the PHPP does not claim to predict the frequency of overheating with a high degree of accuracy; rather, it only roughly assesses thermal comfort in summer, based on the categories given in Table 1. In Section 3.3 it will be explained why a more accurate calculation would not make sense at all.
| h>25 °C | assessment |
| > 15% | catastrophic |
| 10 – 15% | poor |
| 5 – 10% | acceptable |
| 2 – 5% | good |
| 0–2% | excellent |
| Table 1: Classification and interpretation of the frequency of overheating |
Since temperature fluctuations are relevant for calculation of the frequency of overheating, this inevitably entails the use of a dynamic calculation method. In order to avoid a complicated dynamic simulation based on hourly data, a greatly simplified dynamic method is used in the PHPP. Figure 15 illustrates this principle in comparison with a dynamic simulation for the same underlying test reference year. The course of the indoor temperature curve is determined under constant monthly boundary conditions using a 1-output model. There is an exponential indoor temperature curve for each month, the average value of which can be calculated using analytical methods. If the indoor temperature is less than the heating setpoint temperature at the end of the month, the following month starts with the heating setpoint temperature again.
In order to be able to show the influence of individual hot days as well, and to obtain meaningful results for small overheating frequency values, the month of July is additionally divided into several parts: the cooling load day at the end of the month, the four preceding days with slightly lower temperatures and radiation values, another twelve preceding days with lower temperatures and radiation values once more, and the then the rest of the month. In the process, the month is divided in such a way that the monthly average values for the outdoor temperature and solar incidence for July remain unchanged. The average values for the indoor temperature are also determined in the same way for these shorter periods.
The frequency of overheating can now be ascertained from all average values and the respective time periods. Although the temperatures determined using the simplified method differ greatly from the hourly simulation at times, the overheating frequencies correlate exactly for both methods in order to enable classification in accordance with Table 1.
The method according to the PHPP has proved successful for residential Passive House buildings as described above, and the results predicted by the PHPP have always been realised also in the case of office buildings and schools. Any weak points relate above all to buildings with a poor standard of thermal protection. When we consider an uninsulated top floor for example, the solar loads are so high that the temperatures can become unbearable for a few hours of the day. At night the room cools down rapidly so that the daily mean temperature stays within the comfortable range. A method with a time resolution of one day or more generally cannot depict such processes. The PHPP therefore shows a warning if the solar loads for one day are so high that they can no longer be stored in the building mass.
The following questions arise in connection with non-residential buildings:
- How suitable is the method for non-residential buildings with higher and greatly fluctuating loads?
- Shouldn't the result be expressed as the usage period because the hours of overheating always occur during the period of use?
- To what degree of accuracy can the frequency of overheating hours be calculated?
- Can the method be used for individual, possibly critical rooms as well, or only for complete buildings?
3.1 Use in non-residential buildings
The correlation of the simulation and simplified PHPP calculation for use in non-residential buildings with moderate and high internal loads of 3 or 9 W/m² are shown in Figures 16 and 17. A ribbon window facade on one side was assumed in each case, since passive cooling is not possible for fully glazed buildings without any exterior shading in any case.
As might be expected, the frequency of overheating depends greatly on the air change rate of summer ventilation. Differences result mainly with low air change rates and high overheating frequencies in the case of moderate internal loads of 3 W/m². Here the exact value of the overheating frequency results from the average monthly values of the boundary conditions, so that a certain level of inaccuracy is unavoidable. Highly precise results are also unnecessary as it is enough to have certainty of direction and the knowledge that the building is extremely uncomfortable under these conditions.
There is a similar tendency for high loads with 9 W/m². However, for air change rates higher than 3 h-1, the summer ventilation algorithm of the PHPP provides values that are too pessimistic; while the frequency of overheating with a five-fold air change rate is already within the acceptable range according to the simulation, this is not the case with the PHPP. This difference is due to the method used for calculating the removal of heat through summer ventilation. There are still possibilities for refining the calculation method, but the PHPP algorithm is at least on the safe side.
 |  |
| Figure 16: Example with frequency of overheating plotted against air change rate in summer for low internal heat loads | Figure 17: Example with frequency of overheating plotted against air change rate in summer for high internal heat loads |
3.2 Conversion to usage period?
In non-residential buildings, the question of whether all hours with overheating fall within the usage period arises on account of the intermittent usage. If that was the case, then the frequency of overheating determined in the PHPP can (and must) be converted to that occurring during the usage - as a meaningful measure of thermal comfort in summer - using the factor tYear/tUse.
In fact, in many cases this conversion is much too pessimistic. This is apparent even without observing individual examples, when one considers that overheating frequencies of more than 100% are achieved in buildings in which excessive temperatures occur even outside of usage periods.
Figure 18 shows a temperature curve in a fully glazed office with a high air change rate in summer. This graph first and foremost demonstrates that passive cooling is imperative in a room without exterior shading. This was established by both methods equally: according to the simulation, the frequency of overheating was 28%, while this was 44% according to the PHPP. Overheating is mainly caused by solar loads; despite the high air change rate, the building takes just as long to cool down to temperatures below 25°C again at the end of the day as it did to heat up to the maximum temperature before. However, only the heating up phases take place during the usage periods, therefore calculation of the frequency of overheating with reference only to the usage period leads to almost the same result as above, namely 33%. In contrast, conversion of the PHPP result gives a frequency of overheating of 141% of the usage period.
Figure 19 shows a similar example. Here seminar room usage is assumed, with high internal loads, but moderate window areas. The calculations with the simulation and the PHPP correlate well with regard to the entire year.
Based on the entire year and the usage period, the overheating frequencies can differ considerably depending on the air change rates which are possible in summer. Conversion with the ratio of usage period to the entire year would also give pessimistic results, but the difference is no longer as great. The reason for this can be seen in the upper chart in Figure 19, where the temperature curve for high summer air change rate is shown. The excessive temperatures actually occur almost exclusively during the usage period.
 |  |
| Figure 19: Example with frequency of overheating plotted against air change rate in summer for high internal heat loads and seminar room usage. The simulation results are also shown with reference to the operating times, the PHPP results were converted using the factor tYear/tUse The chart above shows the temperature curve in summer and the usage period for high air change rates in May. |
3.3 Accuracy limits for calculating the frequency of overheating
The indoor temperatures in a Passive House in summer depend on several factors. The size (rather than the exact distribution in time, see [Schnieders 2003]) of the summer air change rate is particularly important. Figure 20 (above and centre) shows an example: excessive temperatures barely occur with a summer air change rate of 1.8 h-1. If the summer air change rate is reduced to 0.6 h-1, then the limit temperature is exceeded 16% of the time. In passively cooled buildings, thermal comfort also fluctuates considerably from year to year. In Figure 20 below, the same calculation as in the chart above is shown for the extreme summer of the test reference year. A frequency of overheating of 14% instead of 1% results with a maximum temperature of 31°C instead of 26°C, with otherwise unchanged boundary conditions.
These examples demonstrate that it is generally not possible to make statements regarding thermal comfort in summer which are more precise than those derived from the categories in Table 1. It is difficult to predict even the summer air change rate, because according to the system, it depends more or less on user behaviour. The outside temperatures and wind speeds which are influenced by the microclimate also affect the removal of heat through night-time ventilation. The year-to-year fluctuations in weather are not subject to any influence in any case.
 | 40 %, north, 3 W/m² constant, nSumm = 1.8 h-1: frequency of overheating 1%, maximum temperature 26°C |
 | 40 %, north, 3 W/m² constant, nSumm = 0.6 h-1:frequency of overheating 16%, maximum temperature 29°C |
 | 40 %, north, 3 W/m² constant, nSumm = 1.8 h-1, extreme summer: frequency of overheating 14%, maximum temperature 31 °C |
| Figure 20: Temperature curve in an example room according to weather and air change rate |
3.4 Use for critical rooms
Designers often wish to be able to assess thermal comfort based not only on the entire building but also on the basis of individual, possibly critical rooms. This is understandable but generally isn't possible with separate consideration of a zone; even when carrying out dynamic simulations it is apparent that thermal coupling with adjacent rooms changes summer thermal comfort quite considerably in some circumstances. This fact therefore is not a weakness of the PHPP method, but is due to physical reasons.
Figure 21 illustrates this relationship for the case where the adjacent rooms are cooler. The centre room is examined in the simulation model used here. The examined room has moderate window areas, the summer air change rate is relatively high with 1.8 h-1 so that thermal coupling to outdoor air is comparatively good in relation to that of the rooms above and below. Each of the intermediate ceilings have more than 2 cm impact sound insulation, the U-value is 1.05 W/(m²K).
The upper chart in Figure 21 shows the temperatures for the case where all three rooms in the model are identical (the same internal loads, the same window areas and air changes rates etc.). This case equates to an isolated examination of just one room. Thermal comfort clearly proves to be insufficient in this case. If the windows in the adjacent rooms are removed and the internal heat gains are reduced to 1 W/m², then the temperature here will always be below 25°C. Thus, due to transfer of heat towards the cooler adjacent rooms, the temperature in the centre room under consideration will now be within the acceptable range.
In the opposite case, individually considering a room is just as inadequate (Figure 22). Taken alone, summer thermal comfort in the room under consideration is excellent. However, if the adjacent rooms are intensely uncomfortable on account of full glazing and high internal heat loads, then this will also affect the centre room being examined; the frequency of overheating is now 13%.
 | 40 %, north, 3 W/m² constant, nSumm = 1.8 h-1, extreme summer: frequency of overheating 14%, maximum temperature 30 °C |
 | ditto, ground floor and top floor without windows and with 1 W/m²: frequency of overheating 4%, maximum temperature 28 °C |
| Figure 21: Temperature curve as a function of adjacent rooms, part 1 |
 | 40 %, north, 3 W/m² constant, nSumm = 1.8 h-1:frequency of overheating 1%, maximum temperature 26 °C |
 | ditto, ground floor and top floor, fully glazed with 9 W/m²: frequency of overheating 13%, maximum temperature 30 °C |
| Figure 22: Temperature curve as a function of adjacent rooms, part 2 |
Isolated consideration thus makes less sense, at least in the case of relatively small, thermally well-coupled rooms. Nevertheless, isolated consideration can provide individual verification for the rooms of a building. In principle, it is possible to design cases in which the frequency of overheating in each room is e.g. less than 5% when considered on its own, but where overheating frequencies of more than 5% can be achieved when coupling of two rooms is taken into account; however, this is only an impairment in the criterion “frequency of hours with temperatures greater than 25°C” and ultimately is not of practical significance. Nevertheless, the method described here may result in unnecessary construction costs if the rooms vary significantly in terms of quality. In order to avoid this, it will be necessary to carry out a dynamic building simulation which takes into account the interaction of the individual rooms. The costs for this are quite considerable and difficult to justify in view of the uncertainties that remain on account of unclear boundary conditions (see above).
If one wishes to keep expenditure within reasonable limits, it makes more sense to restrict the frequency of overheating to 5% at the most, by implementing measures (such as shading, increased ventilation) one by one in the critical rooms – which are generally easily identified even without detailed calculations. Isolated but exact examination of individual parts of the building can only provide insights in the case of e.g. large projects where, in extreme cases, parts of the building are connected just by means of a passage.
4 Conclusion
In many cases, the summer behaviour of non-residential buildings can planned reliably using simplified methods such as those implemented in the PHPP, for example. Calculation of the useful cooling demand using the monthly method has proved to be particularly reliable. The limitations of this method are reached only in the case of loads that are greatly concentrated in time. In the PHPP, calculation of the cooling load just provides a daily mean value. This calculation can thus only be applied if it is possible to store the internal or solar loads throughout the day. This applies with loads that are moderate or evenly distributed in time, otherwise more complicated methods on an hourly basis will have to be used. As a rule, one can decide whether a building is sufficiently comfortable even without active cooling based on the calculated frequency of overheating. Irrespective of the calculation method, such calculations only have a limited accuracy, due solely to the variation in the outdoor temperature from year to year. Hence, calculation results must not be overinterpreted.
The apparently obvious and simple conversion of the overheating frequencies into the usage period of a non-residential buildings, based on the assumption that all excessive temperatures occur during the usage period, turns out to be overly pessimistic. Such conversion is only possible if it is assumed that comfortable indoor conditions can be created again under the given boundary conditions immediately after the period of use has ended, otherwise conversion will give results that are hardly more accurate than those that can be obtained without conversion. Applying this method for individual rooms cannot be recommended. The influence of summer ventilation is mostly well-depicted in these models, weaknesses become apparent with high loads and high air change rates.
5 Literature
| [PHPP] | Feist, Wolfgang (Hrsg.): Passivhaus Projektierungs Paket. Darmstadt, Passivhaus Institut, 1998-2012; Passive House Planning Package |
| [DWD 2004] | Christoffer, Jürgen, Thomas Deutschländer, Monika Webs: Testreferenzjahre von Deutschland für mittlere und extreme Witterungsverhältnisse. Selbstverlag des Deutschen Wetterdienstes, Offenbach 2004; Test reference year for Germany for average and extreme weather conditions, published by the German Meteorological Service in Offenbach |
| [Feist 1998] | Feist, Wolfgang: Heizwärmebilanzen nach EN 832 und dem Passivhaus-Projektierungs-Paket: Ein bedeutender Fortschritt für die rechneri¬sche Ermittlung des Jahresheizwärmebedarfs. In: Arbeitskreis kostengünstige Passivhäuser, Protokollband Nr. 13, Energiebilanzen mit dem Passivhaus Projektierungs Paket, Darmstadt, Passivhaus Institut, Dezember 1998; Energy balance based on EN 832 and the Passive House Planning Package: Significant advancement in calculation of the annual heating demand. In: Research Group for Cost-effective Passive Houses. Protocol Volume No. 13, Energy balance using the Passive House Planning Package |
| [Feist 1998a] | Feist, Wolfgang: Passive Solarenergienutzung im Passivhaus. In: Arbeitskreis kostengünstige Passivhäuser, Protokollband Nr. 13, Energiebilanzen mit dem Passivhaus Projektierungs Paket, Darmstadt, Passivhaus Institut, Dezember 1998; Passive use of solar energy in the Passive House. In: Research Group for Cost-effective Passive Houses, Protocol Volume No. 13, Energy balance using the Passive House Planning Package |
| [Schnieders 2003] | Schnieders, Jürgen: Der Einfluss verschiedener Lüftungsstra¬tegien auf das Sommerklima – vergleichende Untersuchung mittels dynamischer Gebäudesimulation. In: Arbeitskreis kostengünstige Passivhäuser, Protokollband Nr. 22, Lüftungsstrategien für den Sommer, Darmstadt, Passivhaus Institut, 2003 The influence of various ventilation strategies on indoor climate in summer - comparative study using dynamic building simulation. In: Research Group for Cost-effective Passive Houses, Protocol Volume No. 22, Summer ventilation strategies |