Table of Contents
Laws of radiation
Properties of thermal radiation

Thermal radiation has the same properties as light in many respects (obviously, since it is electromagnetic radiation which only exhibits longer 1) wavelengths compared to visible light):
- It spreads at the speed of light c! (299 792 458 m/s)
- It spreads in a linear way!
- The law of reflection applies on all smooth, reflective surfaces. Shiny metal surfaces especially reflect heat radiation particularly well. This is impressively demonstrated in the parabolic mirror experiment: a hot body radiates heat which can be bundled into a parallel directed heat ray using a parabolic shaped mirror.
- It can be reflected, absorbed and transmitted (more on that later; potentially the absorption characteristics of surfaces can be quite different in infrared light than in visible light). However, shiny metal surfaces are reflective at all wavelength ranges (even up to γ–radiation when streaking???).
One can obtain a good idea of the characteristics of thermal radiation in the room temperature environment if one observes thermographic images. In this way one can “see” quite clearly how this differs from visible light:
- The longer wavelength (corresponding to a lower frequency) becomes apparent during spectral decomposition (prism or grating) of the heat radiation from an incandescent bulb.
- In the mid-infrared range (thermal radiation in the room temperature environment) most surfaces are “black” or at least dark grey – and not transparent! For example, glass almost completely absorbs medium and longwave IR, while a plastic bag is transparent!
- And … in the thermal spectral range it is almost always “bright”.
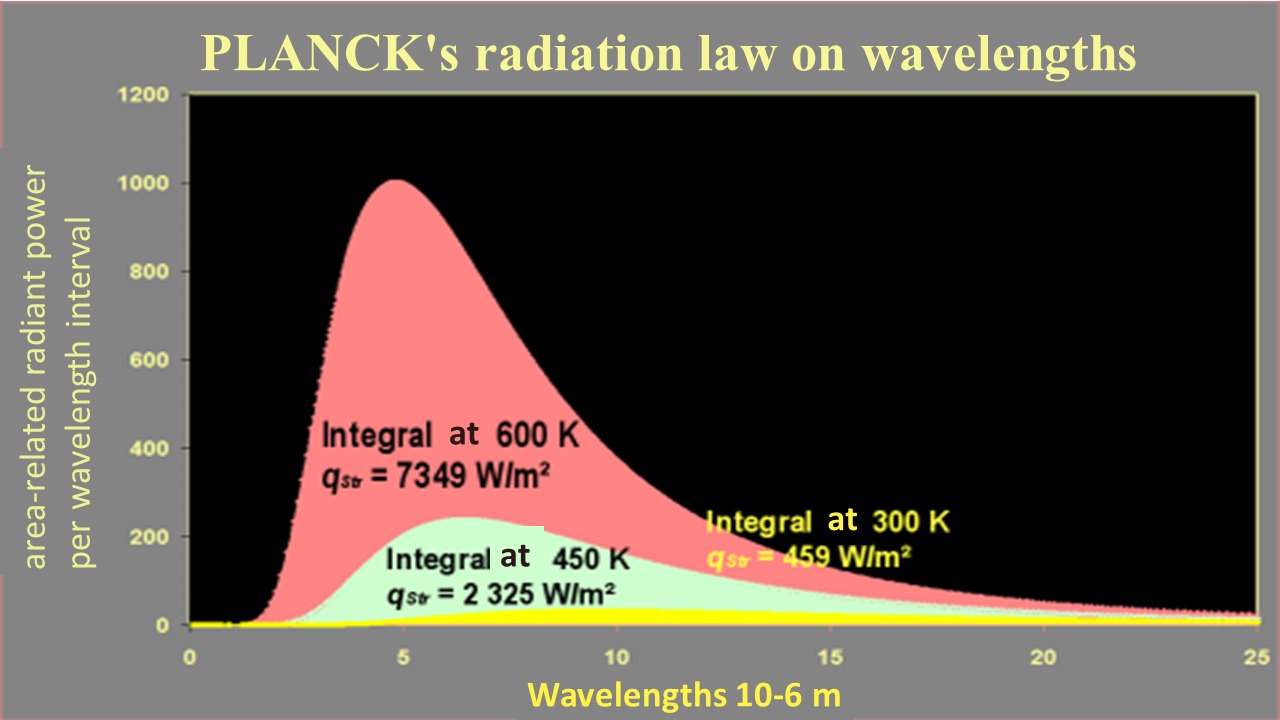
PLANCK's law
In physics, the emission spectrum of an ideal heat emitter (distribution of radiation intensity as a function of the radiation wavelength) was only explained much later on. The fundamental law is known as Planck’s law of thermal radiation. It indicates the radiation intensity/spectral radiance $\dot{q}_{\lambda S}$ that is emitted by an ideal thermal radiator/body with a temperature $T$ at the wavelength $\lambda$. The law itself relies on the almost revolutionary findings of M. Planck: in order to theoretically derive this law, it must be assumed that electromagnetic radiation can only exist in “discrete packets” (called photons) of energy $\varepsilon=hf$ The law is as follows:
${\displaystyle \dot{q}_{\lambda s}= \frac{2 \pi h c^2}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k T}}-1} }$
The two fundamental natural constants $h$ (Planck's constant/quantum of action) and the speed of light $c$ are a part of this. The derivation of Planck's radiation law (German only) can be found e.g. on Wikipedia (Planck's law).
It describes the spectral specific radiance of a black body ˙qλS as a function of the wavelength and the temperature. This law is presented on the right in graphic form for various temperatures. The spectral specific radiance becomes infinitesimally small with both extremely short wavelengths and extremely long wavelengths. It has a maximum at different wavelengths $\lambda_{max}(T)$ depending on the temperature.
Planck's radiation law is the fundamental law for heat radiation. The following frequently applied, more specific laws can be derived from this law, the first through integration across all wavelengths, the second literally by deduction in order to find the maximum.
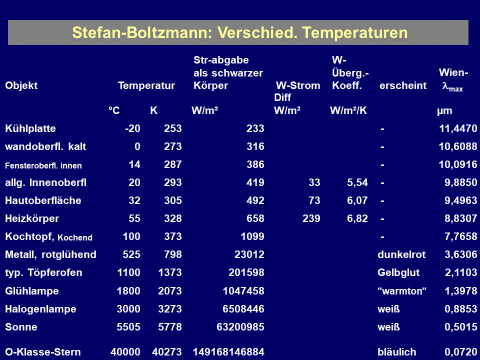
The STEFAN BOLTZMANN radiation law
If we are interested in the total radiation power added up over all frequencies/wavelength ranges, then we must integrate Planck's law across wavelengths from zero to $\infty$. This will give us the total power emitted per unit area
${\displaystyle \dot{q}=\sigma T^4 }$
$\sigma$ is the STEFAN BOLTZMANN constant:
$\sigma$ = 5,670 400(40) $\cdot $ 10-8 W/m²/K4 $\approx$ 5,67 $\cdot $ 10-8 W/m²/K4 “constant of proportionality”. The key point is: the total intensity radiated increases with the fourth potency of the absolute temperature (!)
and the
WIEN's displacement law
$\lambda_{max} \cdot{T} = \text{const}~~~~~~(= 2,897771955... \cdot 10^{-3}$ mK ≈ 2898 µmK )
With increasing temperature, the thermal radiation shifts to increasingly higher frequencies, i.e. shorter wavelengths. Wien's displacement law applies for the maximum of the Planck curve. It was empirically known even before Planck's equation, which however gives the maximum completely correctly.
Example: Sun: surface temperature 5800 K, maximum/peak thermal radiation at 500 nm
Example.: radiant heater: surface temperature 800 K, shallow maximum at 3.6 µm.
Example.: interior wall: surface temperature 295 K, shallow maximum at 9.8 µm.
Example.: freezer: surface temperature 243 K, shallow maximum at 12 µm.
Example.: liquid nitrogen: temperature 77 K, shallow maximum at 38 µm.
Example.: James Webb space telescope MIDI instrument: temperature 6 K, shallow maximum at 493 µm.
Example.: liquid helium: temperature 4.15 K, maximum at 698 µm.
Example.: deep space: cosmic microwave background 2.726 K, maximum at 1.063 mm.
Emissivity
This is the inherent radiation due to thermal movement in a body: for real bodies the specific radiance/emission $\dot{q}_\lambda $ at every wavelength is never greater than with a black body (ideal emitter). It is defined as the emissivity of a body:
${\displaystyle \varepsilon(\lambda):=\frac{\dot{q}_\lambda} {\dot{q}_{Schwarzköper}} }$
The value of $\varepsilon(\lambda)$ is always smaller (or equal) to one. A 'grey body' is a rough approximation for a non-black body. It is characterised by a constant emissivity (independent of the wavelength). The following applies for a grey body: $\varepsilon(\lambda)=\varepsilon $ (=constant). Often we have a situation where emissivity at a certain wavelength range “is high” (an ideal emitter or absorber) and is particularly low at another wavelength (good reflector). We then call such a surface 'selective'. This is often deliberately made so by means of a coating, we then speak of a 'selective coating' - and this creates a large potential for efficient energy applications, as we shall find out below.
In general,
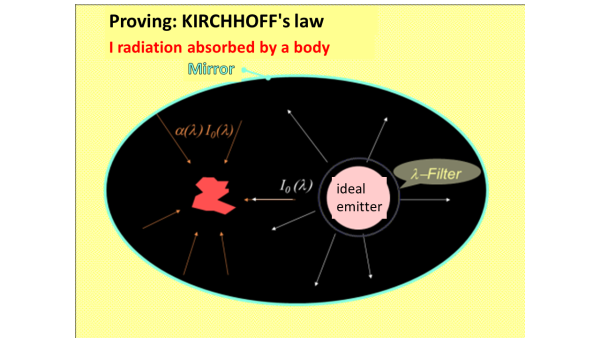
KIRCHHOFF's law of thermal radiation
${\displaystyle \alpha(\lambda)=\varepsilon(\lambda) }$
applies. Emission and absorption capacities are exactly the same size at each wavelength. This is true for every real heat emitter and is a consequence of the second law of thermodynamics; If that wasn't the case, then one of two bodies with the same temperature could heat up at the expense of the other.
Application of radiation laws: infrared thermometer and infrared camera
In principle, measurement of the emitted energy allows the temperature of the radiator to be calculated provided that the emissivity is known with sufficient accuracy. This is generally not the case. For this reason, according to the applicable standards infrared thermometers are not approved for quantitative temperature measurements. Although so-called thermographic imaging (pictures with an infrared camera) provides a graphic overview, a quantitative evaluation requires extensive expertise. Uninformed interpretations can be misleading.
A table with approximate values of typical emissivities has already been compiled under the heating Emissivities. It shows that most surfaces in the chosen environments of human beings have high emissivities (between 85% and 98%) and they reflect very little thermal radiation. So what we record with a thermographic camera is primarily the inherent radiation of the surfaces due to thermal radiation - which in turn is a measure of the temperature. Metallic surfaces are the only exception.
Example of thermal radiators: Quantitatively
The Earth's atmosphere reflects and absorbs other parts of the solar radiation; on a very clear day, 70 to 75% can pass through to the Earth's surface (see “terrestrial solar radiation” in the illustration above). Its maximum lies within the yellow-green range, most of the energy comes from the visible light. However, even in the near infrared range almost half of the energy from the Sun is still received (wavelengths between 750 and 1400 nm). Note: this is the “trick” used in so-called solar control glazing. When we coat a window pane with a material which largely lets the visible spectral range through but which reflects near infrared from approximately 700 nm onwards, then almost half of this energy no longer enters the room although daylight passes through largely unhindered.
Our eyes are sensitive in the visible range. A good window should therefore let the visible spectrum (380-750 nm) pass unhindered as far as possible, so we can perceive our surroundings as usual and the entering sunlight or diffuse light will illuminate the things in our rooms in the normal way. Fortunately, conventional glass exhibits this characteristic to a good extent: it is “transparent” in the visible spectral range as well as in the near infrared range (but any iron that may be present in the glass will result in a greenish tint).
Continue to radiation exchange ️
Here you can also find a derivation of Planck's law of thermal radiation. (German only) This is an insight into a piece of cultural heritage, and the fundamental approach of quantum theory becomes transparent in this derivation. But it doesn't work without mathematics - and for the most important conclusions in building physics, working this out is not a prerequisite. If you are an “expert” you can skip this page for now.